予測不能な空の下で

　「ブラジルで一羽の蝶が羽ばたくと、テキサスで竜巻が起こる」。

この有名な比喩は、ローレンツの発見した「バタフライ効果」を象徴する言葉である。一見、取るに足らないほど小さな変化が、長い時間を経て巨大な結果を生むという現象だ。この考え方は単なる詩的な比喩ではなく、現実の気象シミュレーションにおける数値のわずかな誤差の増幅を意味している。

　1960年代、気象学者エドワード・ローレンツは、気候の時間変化を再現するための単純な方程式を用いて数値計算を行っていた。しかしある日、途中から計算を再開したところ、元の結果と全く異なるシミュレーションが現れた。原因は、入力した初期値の小数点第6位の丸め誤差にあった。彼のコンピュータは0.506127ではなく0.506を初期値として処理していたのである。わずか0.000127の違いが、時間が経つにつれ指数的に拡大し、全く別の気象パターンを生み出した。

　これが「決定論的カオス（deterministic chaos）」の発見であった。

ローレンツ・ストレンジ・アトラクターと今日の天気予報

　ローレンツが用いたモデルは以下の通りだ。（数式等が苦手な方は説明を飛ばしていただいて構わない。）

　水を満たした水槽内に生じる二次元の対流について考える。水槽を下から熱し加熱により水槽内の水は鉛直温度勾配という対流が生じる。Cを「対流の強さ」、Lを「温度差」、Mを「上昇気流の速度」として各定数であるσを「流体の粘り」、rを「温度差の大きさ」、bを「エネルギー損失の割合」とした際、以下のような3本の連立微分方程式が出来上がる。

dC/dt=σ(L-C)、dL/dt=C(r-M)-L、dM/dt=C・L-bM　（tは時間を表す）

　これらの対流の動きを単純化した式に基づき

➀今の値　ｔ　

②変化の速さ（時間変化率）Δｘ/Δt　

③次の時刻　t+Δt　

を組み合わせたうえで定数に値を代入すると解の軌跡は以下のような不思議な形を描く。

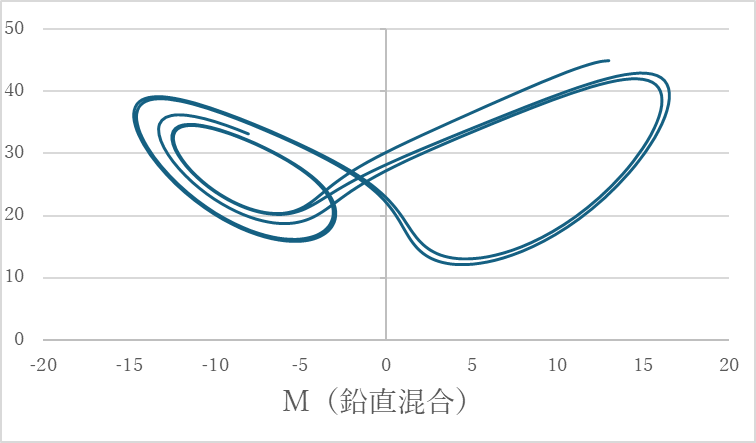
　まるで左右対称の蝶の羽のような軌道だ。この“蝶の形”は偶然ではない。どれだけ時間が経っても、変数C・L・Mの動きはこの形から逸脱せず、しかし同じ軌跡を二度とたどらない。未来の状態は完全に決まっているが、初期値をほんの少しでも変えるとまったく別のパターンに飛んでしまう。完全に決定的なのに、予測不可能というわけだ。

これがカオスの本質であり、気象というシステムの宿命であるのだ。

　話を日常に戻そう。

　我々は毎日のように天気予報を見て、「週末は晴れるかな？」「洗濯物は外に干せるかな？」と考えている。けれど、経験的に知っているはずだ。天気予報は3日後くらいまではかなり当たるのに、1週間を超えると外れることが多い。ではなぜ、わずか2週間先の天気でさえ確実に当てるのが難しいか？

　その理由は、気象という現象が「カオス的」だからだ。

　「カオス」と聞くと「無秩序」や「混沌」をイメージするかもしれないが、科学では少し違う。上で紹介した「ローレンツ・ストレンジ・アトラクター」のように“決まったルールに従って動いているのに、結果が予測できない”という不思議な現象を指すのだ。

　例えば、空気の流れを考えてみよう。もし地球上の空気の動きを、数学的にすべての粒まで正確に把握できたとしたら――理論的には、未来の天気を完璧に予測できるはず。でも、実際にはそんなことは不可能。観測の誤差、気圧や温度の微妙なズレが、数日後にはまるで別の結果を生み出してしまうからだ。

　何が言いたいのか…

　天気が短期間でコロコロ変わるのは、自然が“気まぐれ”だからではなく、自然が繊細すぎるから、2週間先の天気を確実に言い当てることがほぼ不可能ということだ。

温暖化を「断定」することの難しさ

　ローレンツが示したように、わずかな初期条件の違いが未来を大きく変えてしまうのが自然現象の本質である。気候変動の議論でも同じことが言える。地球温暖化をめぐる数値シミュレーションは、膨大な観測データと方程式の上に成り立っているが、その出発点となる「初期値」や「仮定」は完全ではない。たとえば大気中の水蒸気量や雲の分布、森林の吸収能力、火山活動の影響など、いずれも非線形（一次式ではなく高次式を含む数式）な要素を多く含み、微小な差が将来の平均気温を大きく変えてしまう。近年の温暖化モデルは、大気・海洋・陸地・氷床・生態系といった複雑な相互作用を含む多層構造になっている。そのため、単に気温や二酸化炭素濃度だけでなく、人間活動による排出シナリオ、森林破壊、都市の熱環境など、社会経済的な要素まで考慮される。こうした変数は年々変化し、モデルに与える「初期条件」そのものを動かしている。つまり、温暖化の将来予測は“自然の不確実性”と“人間社会の不確実性”が重なり合った問題なのである。

気候モデルは、地球全体を格子状に区切り、それぞれのセルでエネルギーの流れを数値的に追うが、その精度には限界がある。格子を細かくすれば計算は膨大になり、粗くすれば現実から離れてしまう。しかも数十年先、数百年先という長期スパンでは、誤差は雪だるま式に拡大する。ゆえに「2100年の平均気温は○℃上がる」といった予測値は、あくまで「複数の可能性の一つ」にすぎない。

　気象庁が2週間先の天気すら確実に示せないのは、決して技術不足ではなく、自然の構造がカオス的であるためだ。まして数十年先の地球規模の変化を「断定」することは、数理的にも極めて困難である。現在の気候モデルは「どのような傾向が最も起こりやすいか」を示すものであり、「絶対的な未来」を保証するものではない。実際、観測データはこの数十年間、全球平均気温が一貫して上昇していることを示している。北極海の海氷面積の減少、異常高温の頻発、豪雨や干ばつの強度の変化など、気候システムの変動はすでに私たちの生活を脅かし始めている。ただし、その変化の速度や地域的な影響の度合いを“正確に予測する”ことが難しいのだ。

　しかし、それは「温暖化を否定すべき」という意味ではない。むしろ、「不確実性を含めて理解する」ことこそが科学的な姿勢だろう。気候の未来は一本の道ではなく、分岐し続ける無数の可能性の集まり。我々はその中で、より良い選択を探すしかないのだ。

　そして、予測は無意味ではない。ローレンツの蝶が示すように、小さな変化が大きな結果を生むならば、逆に言えば「小さな選択」が未来を左右することもできる。カオスは不確実性の象徴であると同時に、希望の象徴でもある。未来を断定することはできなくても、多くの予測や理論に基づき、話し合い、未来を形づくる行動を考えることが大切だろう。